4369. Поджог

 

Перед Вами самая обычная паутина. Однако, как опытный олимпиадник, Вы сразу заметили, что она представляет собой связный граф с n вершинами и m ребрами. Если поджечь какую-либо вершину, она загорится, через секунду вспыхнут все смежные с ней вершины, затем загорятся вершины, смежные с уже горящими, и так далее.

Вам известно, в каких вершинах одновременно подожгут паутину. Определите, сколько секунд пройдет до возгорания последней вершины и какой будет номер у этой вершины.

 

Вход. В первой строке заданы два натуральных числа n (1 ≤ n ≤ 105) – количество вершин и m (n – 1 ≤ m ≤ 105) – количество рёбер.

В следующих m строках указаны пары чисел u и v (1 ≤ u, v ≤ n), обозначающие вершины, соединённые ребром.

В следующей строке содержится число k (1 ≤ k ≤ n) – количество точек поджога.

В последней строке приведены k чисел – номера вершин, в которых одновременно начинается возгорание.

 

Выход. В первой строке выведите время в секундах, когда загорится последняя вершина. Во второй строке выведите номер этой вершины. Если таких вершин несколько, выведите ту, номер которой минимальный.

 

Пример входа

Пример выхода

6 6

1 2

2 6

1 5

5 6

3 5

4 5

2

1 2

2

3

 

 

РЕШЕНИЕ

поиск в ширину

 

Анализ алгоритма

Для решения задачи следует запустить поиск в ширину из нескольких источников. Поместим все точки поджога в очередь, после чего запустим алгоритм.

 

Пример

Граф приведенный в примере имеет вид:

 

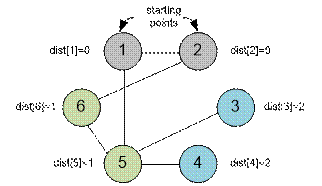
Реализация алгоритма

Объявим рабочие массивы для поиска в ширину.

 

vector<int> dist;

vector<vector<int> > g;

queue<int> q;

 

Функция bfs совершает поиск в ширину. Все источники поиска в ширину уже находятся в очереди q.

 

void bfs(void)

{

  while (!q.empty())

  {

    int v = q.front(); q.pop();

    for (int to : g[v])

      if (dist[to] == -1)

      {

        q.push(to);

        dist[to] = dist[v] + 1;

      }

  }

}

 

Основная часть программы. Читаем входные данные. Строим граф.

 

scanf("%d %d",&n,&m);

g.resize(n+1);

for(i = 0; i < m; i++)

{

  scanf("%d %d",&u,&v);

  g[u].push_back(v);

  g[v].push_back(u);

}

 

Значение dist[i] содержит время, через которое загорится вершина i. Изначально все значения dist[i] полагаются равными -1.

 

dist = vector<int>(n+1,-1);

 

Читаем номера вершин, являющихся источниками поджога. Для каждой такой вершины id устанавливаем dist[id] = 0 и добавляем её в очередь.

 

scanf("%d",&k);

for(i = 0; i < k; i++)

{

  scanf("%d",&id);

  dist[id] = 0;

  q.push(id);

}

 

Запускаем поиск в ширину.

 

bfs();

 

Ищем вершину id, которая загорится последней. Переменная mx содержит время, через которое загорится эта вершина.

 

mx = -1;

for(i = 1; i <= n; i++)

  if (dist[i] > mx)

  {

    mx = dist[i];

    id = i;

  }

 

Сначала выводим значение dist[id] – время, когда загорится последняя вершина. Затем выводим номер id этой вершины.

 

printf("%d\n",dist[id]);

printf("%d\n",id);

 

Java реализация

 

import java.util.*;

 

public class Main

{

  static ArrayList<Integer>[] g;

  static Queue<Integer> q = new LinkedList<Integer>(); 

  static int dist[];

  static int n, m;

  

  static void bfs()

  {

    while(!q.isEmpty())

    {

      int v = q.poll();

      for(int i = 0; i < g[v].size(); i++)

      {

        int to = g[v].get(i);

        if (dist[to] == -1)

        {

          q.add(to);

          dist[to] = dist[v] + 1;

        }

      }

    }

  }

 

  @SuppressWarnings("unchecked") 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    n = con.nextInt(); m = con.nextInt();

   

    g = new ArrayList[n+1];

    for(int i = 0; i <= n; i++)

      g[i] = new ArrayList<Integer>();

   

    dist = new int[n+1];

 

    for (int i = 0; i < m; i++)

    {

      int u = con.nextInt();

      int v = con.nextInt();

      g[u].add(v);

      g[v].add(u);

    }

 

    Arrays.fill(dist,-1);   

    int k = con.nextInt();

    for (int i = 0; i < k; i++)

    {

      int id = con.nextInt();

      dist[id] = 0;

      q.add(id);

    }

   

    bfs();

 

    int max = -1, id = -1;

    for(int i = 1; i <= n; i++)

      if (dist[i] > max)

      {

        max = dist[i];

        id = i;

      }

 

    System.out.println(dist[id]);

    System.out.println(id);

    con.close();

  }

}